
Relic neutrinos—neutrinos of the cosmic neutrino background,
created in the Big Bang—are
the second most numerous particles in the universe. Only photons of the
cosmic microwave background
(CMB) somewhat outnumber them. Relic neutrinos have streamed unimpeded from the first second of
the Big Bang, for hundreds of thousands of years before the
last scattering of CMB photons.
Interacting weakly but neutral to the electromagnetic
and strong interactions, relic neutrinos
have so far eluded direct detection by particle detectors.
However, relic neutrinos also interact gravitationally.
They can therefore be studied en masse through cosmological observations.
To reveal relic neutrinos and determine their properties, it is crucial to identify
their nondegenerate observable cosmological signatures.
These are features in measurable characteristics of the universe that are
produced only by the neutrinos and that are not affected by
changing other cosmological parameters:
the abundance of dark matter and dark energy, the rate of cosmological expansion, etc.
Fortunately, relic neutrinos do provide distinctive nondegenerate signatures.
Specifically, I have determined[1]
that of all known particles and matter species
of the Standard Cosmological Model only relic neutrinos
additively shift[1] the
pronounced acoustic peaks in the CMB power spectrum,
shifting the temporal phase of the acoustic oscillations.
(The “acoustic oscillations" are waves in the slightly inhomogeneous
“photon-baryon" plasma of the early universe: a plasma of photons, electrons, and ions—all interacting
before the electrons
and ions recombined
into a gas of neutral atoms, transparent to the photons, which then became the CMB.
These waves had been sourced by the primordial inhomogeneities, expected from cosmological inflation.
They produced the most prominent
feature in the observed angular power spectrum of the CMB: its
acoustic peaks.)
Paper [1] proved
that (for the standard, inflation-generated cosmological inhomogeneities, called “adiabatic")
the temporal phase of the acoustic oscillations is shifted by and only by the gravitational
impact of the species of particles or other cosmic matter with the following two properties:
(i) the species interact with the photon-baryon plasma only gravitationally;
(ii) perturbations in the species propagate faster than the “acoustic speed",
which is the speed of the acoustic waves in the photon-baryon plasma.
Of the known elementary particles, only neutrinos, freely streaming at nearly the speed of light,
fulfill both conditions.
CMB observations have only recently reached the resolution required
to study relic neutrinos:
• In 2015 the predicted[1]
neutrino-induced additive shift of the acoustic peaks in the CMB
was observed by ESA’s Planck satellite [3,4].
The measurements of the magnitude of the shift in the Planck data confirmed [3,4] my theoretical prediction [1].
• In 2018 the same neutrino-induced shift was also
detected[5]
in the baryon
acoustic oscillations, which are the imprints of the acoustic oscillations in
the photon-baryon plasma on the distribution of galaxies.
• The accuracy of determining neutrino properties with cosmological observations can still be improved
dramatically by raising the angular resolution of maps of CMB temperature and polarization,
the latter being particularly important[1] for studying neutrinos.
Another detectable signature of relic neutrinos, also first shown in [1], is increased
diffusion
damping (a.k.a. Silk damping) of the CMB inhomogeneities on small scales.
The increase of damping is caused by faster expansion
of the radiation-dominated universe whose energy density is enhanced by the relativistic neutrinos.
(The mechanism for the increase of diffusion damping
in the CMB by decoupled relativistic species, including light neutrinos, thus
differs from more familiar smoothing of inhomogeneities
in warm dark matter, e.g., in massive neutrinos,
streaming out of overdense regions into underdense ones.)
Only free-streaming relativistic particles shift the phase of the acoustic peaks.
On the other hand, diffusion damping is affected by the total radiation energy density.
Hence, diffusion damping is also increased by
the relativistic species that contribute to the radiation density but
do not stream freely.
Thus, jointly, the phase shift and diffusion damping of the CMB power spectra let us both measure
the abundance of relativistic species
and constrain their interactions.
The shift of the acoustic peaks and the increase of diffusion damping of CMB anisotropy constrain
the density and interactions of any “dark radiation”: the standard neutrinos as well as
other possible decoupled relativistic particles,
e.g., light sterile neutrinos.
Moreover, these and other found cosmological signatures[2]
of the dark radiation may expose[2]
a scalar field, called
“quintessence”,
as its energy is expected to track
the radiation energy in the radiation-dominated universe,
before the field manifests itself as the dark energy
when the energy density of the matter in the expanding universe exceeds
the redshifting energy density of the radiation.
Technical remark for cosmologists (click to expand/collapse)
Please note that the shift of the phase of the acoustic oscillations in the CMB by neutrinos is not caused
by neutrino anisotropic stress. This incorrect “explanation” of the phase shift is encountered often;
sometimes it is even credited to our paper[1] that discovered the shift and established its origin.
Instead, [1] showed that the phase of the acoustic oscillations shifts
when and only when the Green’s function for gravitational potential at the acoustic horizon is non-zero.
[This is evident from eqs. (119-120) of [1] and is stated in the text below these equations.]
Thus the phase of the oscillations in the CMB power spectrum shits when perturbations in the species
coupled to the CMB only gravitationally propagate faster than sound in the photon-baryon plasma.
Anisotropic stress does not matter: it may be present or absent. Certain underlying phenomena can affect
both the perturbations' speed and anisotropic stress.
The speed and stress are nevertheless independent characteristics of cosmological species.
The example next demonstrates it.
To confirm irrelevance of anisotropic stress for the shift, consider replacing the relativistic neutrinos by dark radiation
in the form of a classical scalar field (early quintessence) of equal background energy density (with the same w=1/3).
The short-wavelengths perturbations in a classical field move at the speed of light,
exceeding the acoustic speed in the photon-baryon plasma.
On the other hand, a scalar field has no anisotropic stress. Despite the absence of anisotropic stress,
the classical scalar field as well shifts[2] the phase of the CMB oscillations. Moreover,
the shift caused by the scalar field — with zero anisotropic stress — is more than
3 times larger
than the shift caused by neutrinos of equal energy density.
This and the more general question of which property of dark species,
including their anisotropic stress, is probed by which parameter of the observable angular power spectra
of the CMB and large-scale structure are studied in detail in arXiv:0707.0692. This preprint has never been resubmitted
(because of some issues at Los Alamos) despite receiving a favorable review from the Astrophysical Journal referee, who
suggested publishing the preprint in the Astrophysical Journal. The preprint is available on the arXiv.
In particular, please note its summary Table 1 on p. 19.
Explanation of the damping enhancement and other details (click to expand/collapse)
The redshift of matter-radiation equality is imprinted on the observed angular power spectra of the CMB
and large-scale structure. With the equality redshift thus fixed to its measured value,
the higher radiation density from additional relativistic species requires higher matter and dark energy densities.
The higher density of the universe entails a greater Hubble expansion rate, which is constrained loosely by direct measurements.
Under the faster expansion, i.e., smaller Hubble distance, the same redshift and angular intervals correspond to smaller physical distances.
On the other hand, the length scale of diffusion damping depends on the photon-electron scattering cross section.
The cross section, known from precise laboratory measurements, is unchanged for the
higher energy density of the universe.
All the quantities relevant to the angular scale of diffusion damping can still be preserved under
increasing radiation density but offsetting the increase of the expansion rate with reduction of
the primordial helium abundance Y
as ΔY/ΔNν ≈ −0.05
[1].
The offset is, however, limited by the constraints imposed on the helium abundance Y
by independent astrophysical measurements and by
Big Bang
nucleosynthesis. With Y determined independently of the CMB,
higher radiation density increases the ratio of the diffusion length scale to the Hubble distance.
Hence additional relativistic species
increase damping of the CMB anisotropy at small angles (Fig. 5 of [1]).
Probing the Structure of Dark Sectors

Various types of invisible matter provide a large or dominant fraction of energy of the universe throughout
its entire evolution: past, present, and future. These “dark” species—dark matter, dark energy,
and dark radiation (the known neutrinos and possibly yet undiscovered relativistic species)—do interact
with the regular matter and light gravitationally.
This lets us unveil the dark species and probe their properties with cosmological observations
of visible matter and light, including the CMB.
We can obtain particularly specific and detailed information about the dark species by examining evolution
of their inhomogeneities, or “perturbations”. Inhomogeneous cosmological dynamics at
various spatial scales depends on (so, tells us about) many more properties
of the dark species than homogeneous—averaged over space, or “background”—dynamics does.
Many dark species, including neutrinos and dark energy, resist gravitational collapse.
Inhomogeneities in such dark species can gravitationally impact visible matter
and light only during their “horizon entry”;
soon after the entry, the inhomogeneities become unobservable.
Moreover, the cosmic microwave background (CMB)—the sharpest of today's
cosmological probes—is most prominently affected by perturbations
in any dark species (including massive and pressureless dark matter[0]) during the horizon entry as well.
[Horizon entry
of an inhomogeneity (of a perturbation) is the time when the expanding
Hubble horizon
had become comparable to the spatial size of the inhomogeneity.
From the start of the Big Bang by the time of horizon entry
light and other interactions had just traversed the inhomogeneity length.]
The standard computer codes, e.g., CAMB
or its predecessor CMBFAST, let us compute the values of many observables
for a given model of dark dynamics. Yet correct computation of observables does not automatically translate
into correct understanding of which property of the dark species affects which observable.
All or most of imprinting of inhomogeneities in the dark species on observables occurs
during the horizon entry. Then evolution is dominated by general relativistic effects and
looks very different,
even qualitatively, when described in terms of different variables that quantify the inhomogeneities.
The so-called “gauge-invariant”[1,2]
or covariant[3,4]
approaches neither eliminate nor even alleviate this ambiguity.
They only replace the choice of gauge—i.e., of coordinates for the curved perturbed spacetime—by the choice of gauge-invariant
variables for quantifying inhomogeneities.
Most of the technically acceptable and popular descriptions do not reflect explicitly the cause-effect
relationship between properties of dark species and features in measurable cosmological distributions that are affected by those properties.
We can correctly compute observables with any description. Yet most descriptions, including
those being taught in most cosmology classes and used most widely,
lead to erroneous conclusions about the origin of crucial visible
features.[0]
In contrast, [5] proves mathematically that the descriptions of weakly
inhomogeneous cosmological evolution that satisfy two simple and natural criteria render the objective
causal dependencies directly. At the same time, the dynamical equations and their solutions in a
formalism[8] that fulfills these two criteria
simplify remarkably.
Deeper than being an illustration, this is equivalent to the distinction between the heliocentric
and geocentric descriptions of the solar system.
In general relativity, no coordinate frame for arbitrarily curved spacetime is fundamentally preferred.
Yet the inertial frames become physically preferred in the limit of weak gravity.
Only in them do velocities of free objects remain unchanged without influence of other bodies.
Hence any change of the velocities of planets, comets, etc. in an inertial frame is objectively caused
by influence of other physical bodies: the Sun, other planets, etc.
One could specify the dynamics of the solar system and crunch it with computers in the non-inertial
geocentric frame, adding the centrifugal and Coriolis forces. Yet the resulting
description—the Ptolemaic system with epicycles—obscures the causal connection between the path of planets, comets, etc.
that we see on the sky and the gravitating bodies that shape the observed path.
Also, the non-inertial geocentric frame yields more complicated equations and unwieldy solutions.
Likewise, certain variables for cosmological perturbations become physically preferred in weakly inhomogeneous
expanding space (weakly perturbed FLRW metric).
These variables do not change without an objective—locally measurable and gauge-independent—source
that causes the change.[0,7]
This criterion distinguishes the suggested, physically preferred variables
from the traditional variables, used historically as seemingly “natural”, as the geocentric
Ptolemaic view of the solar system once also seemed to be. As with the Copernican view,
the requirement of “a change only by a cause" streamlines the formalism, simplifies the equations and their solutions
substantially
[e.g., slides 11-13 here].
Then the solutions—as proven in [0,
7]—manifestly point at the characteristics
of the CMB and galaxy distributions that map to specific internal properties of the dark species.[5]
These solutions also reveal new signatures[8]
of the dark dynamics that are subtle yet nondegenerate, hence are particularly valuable.
The suggested variables[8]
are the physical perturbations of density, intensity, phase-space distribution, etc.
on subhorizon scales—for microscopic, terrestrial, and galactic distances.
Yet on the cosmological scales comparable to and exceeding the
Hubble horizon,
where general relativity becomes essential, these variables evolve substantially simpler than the traditional variables do:
qualitatively simpler and by simpler equations [see
slides 11-13].
They are well defined for any species—particles, fields, and any other—through the species’
energy and momentum.
(They are also simply related to the “conserved” Bardeen
curvature[9] ζ,
standard for quantifying superhorizon perturbations, and to its
generalization[10]
for individual species.)
Then we find that some past views should be changed substantially
for understanding the actual origin of even the most prominent and physically
important features in the observed cosmological distributions.
For example, the traditional formalism “shows” that the pronounced enhancement of the first acoustic peak in the
CMB angular power spectrum Cl
relative to the
Sachs-Wolfe plateau at small multipole values l is mainly caused by
the “resonant radiation driving”[e.g., 11,12,13,14].
This is incorrect. No resonant boost of the small-scale
CMB power by radiation objectively
exists[0].
Indeed, if “resonant radiation driving” were real then the measured CMB anisotropy on small
scales—at the first and higher acoustic peaks—would be sensitive to dynamics of the
radiation.
It is not the case: (click to expand)
Over 40% of the radiation energy is, in fact, carried by neutrinos,
whose dynamics substantially differs from the textbook “radiation fluid”.
Yet the cosmological signatures
of the abundant neutrinos are very mild.
Besides, they are
qualitatively different
from those suggested by “resonant radiation driving” of the CMB.
Likewise, the signatures[7]
of possible dynamical early dark energy are much milder and are dissimilar to
those expected from the physically incorrect “resonant radiation driving” picture.
On the other hand, the suppression of the CMB power on large
scales, for l’s below the first acoustic peak, is highly sensitive to evolution
of inhomogeneities in dark matter.
The gravitational potential of dark matter perturbations is the main
reason[0] for the suppression.
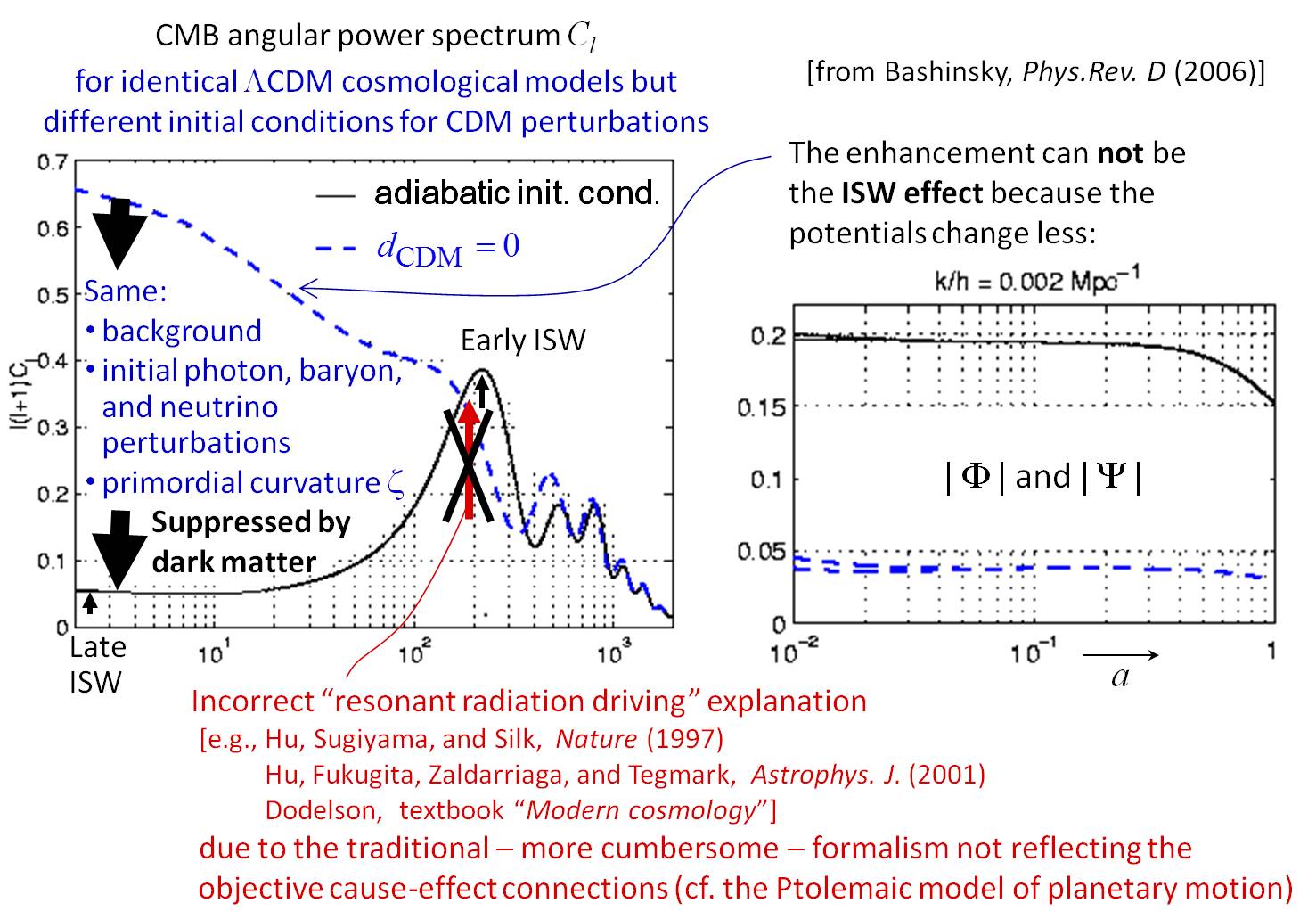 This suppression (non-integrated Sachs–Wolfe effect) is much stronger[0]
than suggested by the description in terms of the traditional variables.
The numerically computed[0] CMB power spectra, displayed on the plots,
confirm this:
This suppression (non-integrated Sachs–Wolfe effect) is much stronger[0]
than suggested by the description in terms of the traditional variables.
The numerically computed[0] CMB power spectra, displayed on the plots,
confirm this:
We would not offer the Ptolemaic system as the primary description of planetary dynamics in today’s
undergraduate astrophysics courses. In graduate cosmology too, it is time to stop explaining the general
relativistic evolution that shapes the anisotropy of the CMB and large scale structure of the
universe — the pillars of contemporary precision cosmology — by similarly misleading
and technically cumbersome formalisms. Encouragingly, some cosmology groups at prominent universities
are adopting[15,
16] the more direct and simple approach.
There is overwhelming evidence from an array of independent cosmological observations that the expansion of our universe
is accelerating. Empirical support for acceleration of the cosmological expansion is provided by observations of type Ia supernovae, CMB anisotropy,
growth of the large scale structure of the universe, ages of galaxies versus their redshifts,
etc.
The cause of the acceleration, however, has so far no universally accepted theoretical explanation.
The most popular alternatives are:
(i) “dark energy”—a new form of matter with large negative pressure;
(ii) “modified gravity”—deviation of gravitation laws from general relativity on cosmological scales.
Surprisingly, the task of empirically distinguishing these, superficially dissimilar, scenarios is extremely subtle.
We cannot differentiate between them, even in principle, by measuring global characteristics of the universe
and their change with redshift:
the rate of cosmological expansion at various redshifts or the global curvature. Neither can we distinguish
between dark energy and modified gravity by observing inhomogeneities in the cosmic microwave background (CMB)
and in other visible matter on large scales where inhomogeneous evolution is linear.[1]
Alikeness of detectable signatures of dark energy and modified gravity is deeply rooted.
Suppose that the acceleration of the cosmological expansion is caused by modified gravity.
Let the dynamics of the visible matter and light remain generally covariant, i.e.,
obey the standard equations of motion in somehow curved spacetime.
Yet let the curvature of spacetime,
and so the gravitational forces that act on the visible species, be not determined by the Einstein equations of general relativity.
Nevertheless, then we could still “explain” all cosmological observations
with the Einstein equations by adding to the visible species some “effective” dark species.[2]
Namely, any curved spacetime admits an effective energy-momentum tensor[2]
that relates to its curvature exactly as the Einstein equations prescribe.
This tensor is covariantly
conserved,[2]
as the energy-momentum tensor would be in general relativity.
Thus even in a modified-gravity universe, not governed by general relativity, assumption
of general relativity and dark species yields correct motion of the visible matter
and light as long as the distribution of energy and momentum of the visible and hypothesized dark species
is set by the effective energy-momentum tensor.
In particular, all the observable manifestations of dark energy
with any possible internal dynamics and of modified gravity
can be described by the same independent phenomenological parameters for
the general conserved energy-momentum tensor.[2]
With this surprising finding, we may ask: Is general relativity even falsifiable?
It is. Definitive methods to distinguish modified gravity from dark energy via cosmological observations
were originally
explained in my paper [2].
Modified gravity can be detected by establishing that the dynamics of the effective “dark species”,
introduced to reconcile the observations with the Einstein equations, should strongly depend on the distribution
of visible matter: more strongly than possible from coupling of the dark and visible species
only gravitationally.[2]
Modified gravity can also be detected by concluding that to explain observations with
Einstein’s general relativity, the inferred “dark species” have to move
superluminally.[2]
At last, general relativity can be falsified by nonstandard phenomenology of gravitational waves.
A note on history [Hu and Sawicki PRD (2007)] (click to expand/collapse)
The described fundamental results on observationally distinguishing dark energy and modified gravity
were later also presented by Wayne Hu, familiar with my paper, and Ignacy Sawicki in
[3].
The marked pages at the following links compare the description of these results in Hu and Sawicki's [3]
and in my earlier paper [2]:
The entire
description of this topic in [3] (file in pdf)
versus
The
equivalent sentences in [2] (file in pdf)
Manifestly, every statement in Hu and Sawicki's [3] related to these results
appeared earlier in [2]. Their paper was by no means written independently.
After posting my preprint on astro-ph, I gave it to Wayne Hu when we both
attended Santa Fe 07 Cosmology Summer Workshop.
He fully read at least its abstract, describing these key results, in my presence and
the presence of several other workshop participants.
It is regrettable when the credit for my results
in [2]
is given to Hu and Sawicki [3]
without mentioning the original work [2].
Not citing the original paper [2] cannot be excused by its being unpublished.
The manuscript [2] was under review in the Astrophysical Journal when the authors
of [3], familiar with [2], neglected to give it due credit while presenting its results in their own publication.
The very first
referee's report,
unfortunately received too late, was already
favorable
and recommended the paper for publication in the Astrophysical Journal.
The manuscript has never been resubmitted and thus formally published because of
issues at Los Alamos National Lab
unrelated to the manuscript or its topics.
Decoding the CMB anisotropy
Anisotropy of the cosmic microwave background (CMB) contains rich information
about the history and composition of the universe, from its birth in inflation
to its presently accelerating expansion and ongoing formation of galaxy clusters.
Some of the information in the CMB reflects the abundance and internal properties of dark species.
The CMB decoupled
around a redshift z≈1,100. However, the CMB sensitively probes the dark dynamics
well after and—even more so—well before its decoupling, up to a redshift of the order of
z∼105.[1]
Indeed, inhomogeneities in any dark species gravitationally affected the CMB most of all
when the inhomogeneities were entering the Hubble horizon,
not when the CMB was decoupling.
For decoding these imprints,
understanding of causal dependencies
in the general relativistic interaction on large scales is crucial.
The
cosmic-variance limit on the accuracy of determining physical quantities with CMB observations
improves dramatically toward high redshift.[1]
There, the accuracy is limited only by the present angular resolution of CMB detectors
and noise-removal techniques.
Evolution of Clusters of Galaxies
Cosmological evolution in recent time—i.e., at small redshift—is highly nonlinear.
Semi-phenomenological approaches, such as proposed by
Press and Schechter
and extended by others (notably,
Bond, Cole, Efstathiou, and Kaiser), let us understand nonlinear evolution intuitively.
Its accurate study however requires numerical simulations. It is worthwhile to explore:
(a) how various limitations and approximations of the simulations affect their accuracy and reliability;
(b) how to understand results of the simulations in terms of simple dynamics-based considerations;
(c) how to develop the most accurate and fast simulation for given computational resources.
Cosmological inhomogeneities—or perturbations—are typically analyzed through their
Fourier decomposition into harmonic waves. An alternative and useful approach is to decompose
the inhomogeneities into spatially localized Green's function. These methods are complementary,
each offering its own advantages and highlighting different physical phenomena.
The Green's function technique is more explicit for phenomena that involve spatial
transport of particles or energy. For example, Green's functions led to new results in studies
of CMB acoustic waves, freely streaming neutrinos, and relic gravitational waves.
In particular, Green's functions yielded the first analytic solution for evolution of cosmological
perturbations that accounts for decoupled relativistic neutrinos (for both
scalar[1] and
tensor[2]
modes). They also helped notice that the acoustic waves in the CMB produce a narrow
feature[3]
in the real-space auto-correlation functions of the CMB temperature and galaxy
density.[3]
Gravity Waves, Neutrinos and Superluminality

I also applied my technique of plane-parallel
cosmological Green's functions to determine the evolution of
relic gravitational waves
that interact with relic neutrinos.
This produced the first analytic solution[1] for their coupled evolution.
The analytic solution confirmed noticeable (about 40%) suppression,
found originally by Steven Weinberg numerically[2], of the tensor—primordial gravitational waves—power spectrum
on short scales by the streaming neutrinos.
The Green's function solution first determined that neutrinos do not affect the phase of the oscillations
in the tensor power spectrum—a characteristic of primordial gravitational waves that may be
measured with CMB polarization.
The solution revealed yet another previously unknown result[1]:
the phase of the oscillations in the tensor power spectrum could deviate from zero only due to a substance
that supports physical
superluminal propagation.
Technical remark for cosmologists (click to expand/collapse)
The Green's functions paper [1]
calculated the reduction of the amplitude of the tensor power spectrum by neutrinos in the first order
of expansion in ρν/ρtot.
It nevertheless derived the aforementioned, new results for the phase shift to all orders.



 This suppression (non-integrated Sachs–Wolfe effect) is much stronger
This suppression (non-integrated Sachs–Wolfe effect) is much stronger



