Generically emergent quantum fields
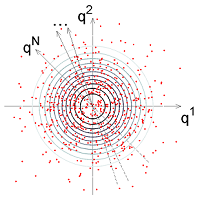
Consider a large collection of arbitrary static objects. Let each of the objects be characterized by many properties that are quantifiable by real numbers. For example, we may consider all the planets in the visible Universe and take such their properties as mass (q1), radius (q2), radius of the core (q3), the amount of carbon in the atmosphere (q4), etc. Properties qp of objects familiar to us obey a distribution that is specific to their nature. However, general linear combinations of many independent properties qn = ∑p cnp qp are distributed by the universal normal (Gaussian) law, at least, under the conditions of the central limit theorem. Some N such generically chosen uncorrelated coordinates qn are therefore distributed similarly to the picture on the left. For the earlier example, every red dot in the picture would represent the values of the generic coordinates qn for a particular planet.
At imperfect resolution the density of the dots in the picture can be approximated by a smooth function. By the above, we may fit it by a Gaussian function. Let us regard this smoothed density of the generic properties qn as a material representation of the Heisenberg-picture wave function of the modes of an inflating field for the simplest, textbook model of cosmological inflation with a potential mφ2. For the degrees of freedom of the inflating field we may take the amplitudes of the field modes φ(k) with various wavevectors k. Then φ(k) at an initial time are the arguments of the field's wave function ψ(φ(k)). Let us identify the variables φ(k) with the coordinates q of the generic basic distribution above: φ(kn) = aqn. (The proportionality factor a(kn) depends on the chosen Hamiltonian for the field; e.g., see Sec. IV.D of the main paper.) Since by construction we identified the wave function ψ(φ(kn)) with the smoothed generic distribution, it is approximately Gaussian. By our definition of φ(k), the field modes are initially in the ground state of the taken inflationary potential.
At later times, the quantum field operators φ̂(k) undergo the standard Heisenberg evolution by the Hamiltonian of the considered field theory. In the Heisenberg picture, the field wave function does not evolve and remains materially represented by the smoothed generic basic distribution. The quantum states of the emergent physical world are the various decoherent Everett branches[1] of this overall wave function. They roughly correspond to the projections of the overall wave function on the eigenvectors of the evolved field operators, φ̂(k,t).
Origin of quantum-mechanical probability
In the Copenhagen interpretation of quantum mechanics the Born rule for the probabilistic collapse of the wave function is an ad hoc postulate. But by Bell's theorem this collapse must be nonlocal and superluminal, i.e., irreconcilable with the relativity principles. The Everett (many-worlds) interpretation of quantum mechanics discards the awkward collapse postulate, unnecessary to describe phenomenology. But then all the decoherent evolution branches should physically exist regardless of their norm. Hence even the Everett interpretation requires additional principles[e.g. 2 or 3] that would relate the probability of our following a particular branch to its quantum-mechanical norm.
Let us return to the generic distribution, illustrated above. A statistically significant smooth fit ψ(q) for the basic discrete distribution has easily quantifiable intrinsic uncertainty (see Sec. III of the main paper). An analogy is the uncertainty in the smooth boundary of a macroscopic physical body, composed below certain resolution of almost point-like electrons and nuclei. Once a smooth Everett's branch ψi(q) of the overall fit ψ = ∑i ψi thins below this intrinsic uncertainty, the branch ψi stops being physically real. It is no longer an objective smooth constituent of the displayed discrete arrangement of the dots. The lower limit on the norm of a physical branch makes the number of the branches countable and the probability to live in a given branch unambiguous.
Although it might seem that, in the spirit of the "Level IV multiverse" proposal[4,5], we could apply any conceivable Hamiltonian to evolve the field operators φ̂(k,t), over whose time-dependent eigenvectors we decompose the overall static wave function, essentially the opposite is true. We arrive at strict and concrete limitations on the physical laws and the type of quantum fields that emerge in the generic static distribution.
We prove that a typical internal observer of a typical quantum field system should see the fields masses and couplings changing arbitrarily during evolution. For hypothetical inhabitants of this system the physical laws change inherently unpredictably on every timescale. Then not only the familiar chemistry-based life is impossible but, most generally, the information that the system's inhabitants could gather about their present environment is irrelevant to their future. The "selection of the fittest" of biological evolution is hardly imaginable when the fitness criteria alter rapidly and unpredictably.
The standard anthropic principle, assuming a multitude of worlds with various Hamiltonians, is insufficient to resolve this paradox. Sec. II of the paper proves that even in an anthropically suitable world other Hamiltonians with varying constants have to describe the immediate future of a typical observer. The proof assumes only validity of the quantum superposition principle on the accessible scales, and experiments leave practically no room to doubt it. Then the question concerns our own world: With all the various choices for future physical dynamics that should materialize here and now, why do our physical laws remain unchanged?
Fortunately, among the various quantum field systems that emerge generically as described, there are special ones whose Hamiltonian cannot be modified without destroying the system. These systems possess local dynamical symmetries, including the gauge and diffeomorphism symmetries of the observed world. In other words, they have the standard gauge interactions of elementary particles, full (quantum) gravity, and possibly (dynamically broken) local supersymmetry. These emergent systems, looking like our physical world, are not merely a theoretical invention. They exist as tangible distinctive structures among the objects that surround us.
Initial conditions for quantum cosmology
The paper shows that phenomenologically acceptable and objectively existing emergent worlds evolve from cosmological inflation. This is what numerous cosmological observations also strongly suggest for our universe. The paper demonstrates that even for interacting fields, their high-frequency modes necessarily and naturally start evolving at the Planck scale from the ground state of the interacting Hamiltonian.
Conclusions and consequences
Generic collections of almost arbitrary objects thus objectively contain patterns that represent wave functions of realistic quantum-field systems. These emergent systems are naturally composed of bosonic and fermionic quantum fields of various spin. They evolve by concrete and tightly restricted physical laws with gauge interaction, quantum gravity, and even local supersymmetry. They give from the first principles, without need for postulates, probability for alternative outcomes of quantum processes. Their evolution begins naturally from cosmological inflation. These systems are more than a mathematical theory: their tangible representations exist objectively around us. To the extent studied, these systems appear identical to our quantum, generally covariant, inflation-born physical world.
The emergent quantum evolution is necessarily Everettian. Yet for a finite underlying structure the number of objectively existing Everett branches, while possibly huge, is finite. The branches whose norm diminishes below a fixed positive threshold cease to exist as physical entities. This has important real-world consequences, not only for remote future but for our present.